Linear Equations (Part 1) - Differential Equations Notes

Definitions and Characteristics

First-Order: The first derivative is the highest derivative appearing in the equation.
Linear: The dependent variable (output) $y$ and its derivative $y'$ must appear linearly. No terms like $y^2$, $y y'$, or $(\mu')^2$.

Examples

$P(3-P)$: Not linear because it expands to $3P - P^2$.
$F = mx''$: Linear, but not first-order (it is second-order).
$A' + e^t A = \cos(t)$: Linear first-order where $A = A(t)$.
$A' + t^3 A = t^7$: Linear first-order.
$A' + t^3 A^2 = t^7$: Not linear because of the $A^2$ term.

Motivation: Mixture Problems

A technical diagram of a mixing tank model used for differential equations, showing inflow from a pipe above and outflow from a pipe at the bottom right.

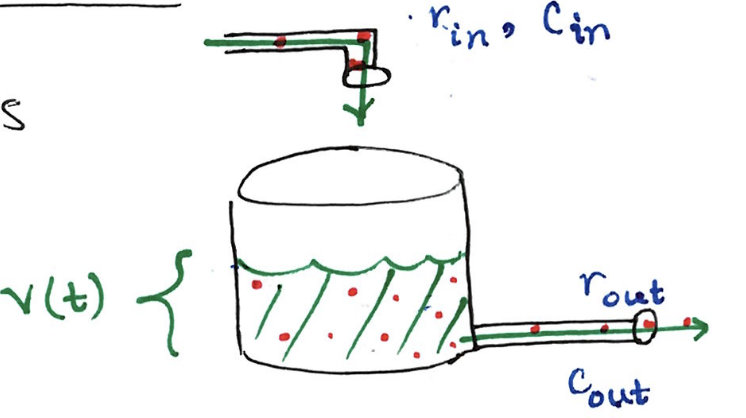
The goal is to model the amount $A(t)$ of a substance in a solution over time.

$v(t)$: Volume of solution (L, gal, etc.)
$r_{in}, r_{out}$: Flow rates (gal/min, L/hr, etc.)
$c_{in}, c_{out}$: Concentration/Density (kg/L, lbs/gal, etc.)

The change in amount $\Delta A$ over a small time interval $\Delta t$ is given by:

$$\Delta A = (r_{in}c_{in} - r_{out}c_{out})\Delta t$$

Taking the limit as $\Delta t \to 0$:

$$\frac{dA}{dt} = r_{in}c_{in} - r_{out}c_{out}(t)$$

If the solution is "well-mixed," we assume $c_{out}(t) = \frac{A(t)}{v(t)}$. The resulting Ordinary Differential Equation (ODE) is:

$$\frac{dA}{dt} + \frac{r_{out}}{v(t)}A(t) = r_{in}c_{in}$$

This follows the standard form: $y' + P(x)y = Q(x)$.

Solving the General First-Order Linear Equation

General form: $\alpha(x)y' + \beta(x)y = \gamma(x)$

Standard Form: Normalize by dividing by $\alpha(x)$ to get:

$$y' + P(x)y = Q(x)$$

The Integrating Factor Method

Find the integrating factor $\rho(x) = e^{\int P(x) dx}$.
Multiply the standard form equation by $\rho(x)$:
$$\rho y' + \rho P y = \rho Q$$
Recognize the left side as a product rule: $(\rho y)' = \rho Q$.
Integrate both sides and solve for $y$:
$$y = \frac{\int \rho Q dx + C}{\rho}$$

Example 1

Find a general solution for $y' - y = 3e^{-x}$.

Step 1: Identify $P(x) = -1$ and $Q(x) = 3e^{-x}$.
Calculate $\rho = e^{\int -1 dx} = e^{-x}$.

Step 2: Multiply and integrate.
$(e^{-x} \cdot y)' = e^{-x}(3e^{-x}) = 3e^{-2x}$
$e^{-x} y = \int 3e^{-2x} dx = -\frac{3}{2}e^{-2x} + C$

Step 3: Solve for $y$.
$y = -\frac{3}{2}e^{-x} + Ce^x$

Example 2

Find a general solution for $xy' - 5y = x^6 \cos(x)$.

Standard form: Divide by $x$ to get $y' - \frac{5}{x}y = x^5 \cos(x)$.

Step 1: $\rho = e^{\int -\frac{5}{x} dx} = e^{-5 \ln|x|} = x^{-5}$.

Step 2: $(x^{-5} y)' = x^{-5}(x^5 \cos(x)) = \cos(x)$.
$x^{-5} y = \int \cos(x) dx = \sin(x) + C$

Step 3: $y = x^5 \sin(x) + Cx^5$.

Initial Value Problem (IVP)

If given $y(\pi/2) = 0$:
$0 = (\pi/2)^5 \sin(\pi/2) + C(\pi/2)^5$
$0 = (\pi/2)^5 (1 + C) \implies C = -1$.

Solution: $y(x) = x^5(\sin(x) - 1)$. Oscillating curve that expands in amplitude as it moves away from the y-axis, representing the function y = x^5(sin(x)-1).